24.3. Neurons to Neural Networks#
So far, we have seen that a single neuron can take multiple inputs, compute the weighted sum of the inputs, and pass the result through an activation function to produce an output. A neural network is simply a collection of neurons arranged in interconnected layers, where each neuron plays a role in the overall computation of the output. You can think of what you have already learned as the simplest neural network—a single neuron. Thus, a sigmoid neuron makes a neural network that you have already seen: the Logistic Regression model!
In this section, we learn the architecture of a neural network and how neurons are organized into layers to create powerful computational systems.
The figure below represents a neural network with three input nodes, one layer of five computational neurons, and one output neuron.
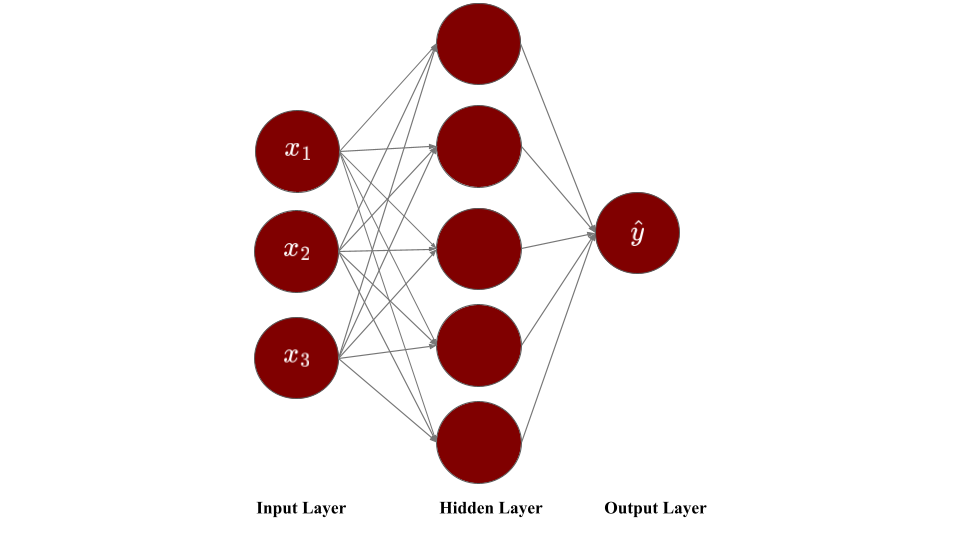
Figure: Single Layer Neural Network
Modern neural networks typically have multiple layers and are called multilayer neural networks. The figure below represents a multilayer neural network with three input nodes, three intermediate layers of computational neurons (with 5, 4, and 5 neurons respectively), and one output neuron.
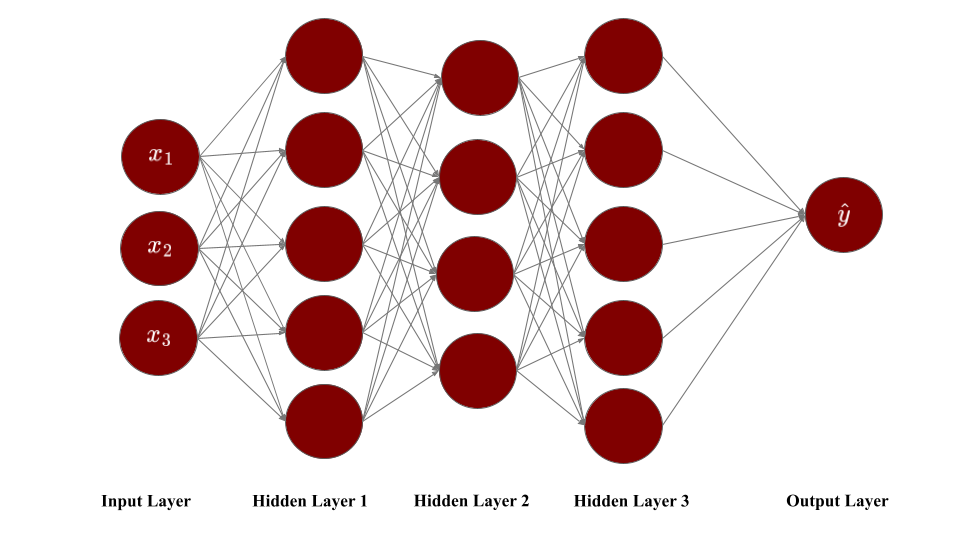
Figure: Multilayer Neural Network
In the neural networks shown in the figures above:
Information flows in one direction—from input to output—without any loops or cycles. This is called a feedforward neural network. The output of every neuron in one layer is passed as input to neurons in the next layer. Each layer transforms its input and passes the result forward until we reach the final output layer.
Each neuron in a layer is connected to all neurons in the next layer. This is called a fully connected or dense neural network. This is one of the most common architectures. Other patterns also exist, such as convolutional networks (where neurons connect to only local regions) and recurrent networks (where connections can form loops).
Let’s learn some terminology related to the neural network architecture.
Input layer: The leftmost layer consists of input neurons and is called the input layer. Each neuron in this layer corresponds to a feature or explanatory variable in your data. These neurons do not perform any computations and simply pass on the input values to the next layer.
Output layer: The rightmost layer consists of output neurons and is called the output layer. It represents the final predictions generated by the model. The neurons in this layer perform computations by applying activation functions to weighted sums of their inputs. In a regression problem or a binary classification problem, where a single output value is expected, there is only one neuron in the output layer. In a multi-class classification problem, the number of output neurons equals the number of categories.
Hidden layers: All the layers between the input and output layers are called the hidden layers. Like the output layer, these layers consist of neurons that perform computations by applying activation functions (like sigmoid, ReLU, etc.) to weighted sums of their inputs—the same computations you saw in the previous section. A neural network can have one or more hidden layers, and each layer can have the same or a different number of neurons. Hidden layers allow the network to learn complex patterns in the data by building representations where early layers detect simple features and deeper layers combine them into more abstract concepts.
Connections and weights: Each connection between neurons has an associated weight that determines how strongly one neuron influences another. During training, the network learns optimal values for these weights.
Bias: In addition to connection weights, each neuron in the hidden and output layers has an associated bias term. Note that input layer neurons do not have bias terms since they perform no computations.
Note
When a neural network contains a “deep” stack of hidden layers, it is called a Deep Neural Network. The field of Deep Learning refers to training neural networks that contain many hidden layers. But how many layers qualifies as “deep”? In the 1990s, a neural network with more than two hidden layers was considered deep. Nowadays, it is common to see neural networks with dozens or even hundreds of layers, so the definition of “deep” is quite fuzzy.
A lot of the time, the terms “Neural Networks” and “Deep Learning” are used interchangeably and sometimes simply mean a neural network, whether deep or not.
An important question: if both shallow wide networks and very deep networks are possible, how do we choose the right architecture?
Why not use a single hidden layer? The Universal Approximation Theorem in machine learning states that a neural network with a single hidden layer containing a sufficiently large number of neurons can approximate any continuous function to any desired degree of accuracy. However, while this theorem guarantees that an appropriate network exists, it doesn’t tell us how to find the right parameters or how large the network needs to be. In practice, deeper networks often learn better representations with fewer total parameters than shallow but very wide networks. In deeper networks, the early layers learn simple patterns and deeper layers combine these into increasingly abstract representations, making them effective for complex tasks like image recognition and natural language processing.
Why not use very deep networks for every problem? While deeper networks can capture more complex patterns, they require more computational resources, energy, and time to train. This creates a practical trade-off between model accuracy and computational constraints. We should choose architectures that achieve acceptable accuracy without excessive cost.
